Bestaat het broeikaseffect nu wel of niet
Inleiding
In een vorig artikel heb ik vrij stellig beweerd dat het broeikaseffect voor de Aarde wel bestaat maar lang niet zo sterk is als aangenomen. Waarom hier op terug willen komen met een volgend artikel? Daar zijn diverse redenen voor. Een zeer geldige reden is dat je nu eenmaal artikelen dient te publiceren op je webblog anders blijven je volgers weg. Dit is een heel geldige en legitieme reden. Je houdt er een weblog op na om je volgers en lezers te behagen. Maar dit is niet de enige en beslist niet belangrijkste reden. De reden dat ik terug kom op de vraag of het broeikaseffect al dan niet bestaat is dat er de nodige ongerijmdheden bestaan in de gangbare voorstelling van zaken. Deze probeer ik in dit artikel uit de weg te ruimen. Hierbij komen de volgende vragen aan de orde. Heeft de Aarde een broeikaseffect? Heeft de de Aarde dit wel nodig? Wat is het broeikaseffect? En hoe toon je dit aan? Veel vragen maar zijn er ook antwoorden. Dit is het doel van dit onderzoek: Heeft de Aarde een broeikaseffect? Om deze vraag te beantwoorden vergelijken we verschillende modellen. Deze modellen zijn uitwerkingen van het beroemde model van Stefan-Boltzmann dat het verband weergeeft tussen stralingsenergie en temperatuur. We beginnen met het gangbare model uit de literatuur en voegen hier de gangbare energiebalans aan toe. Het een zonder het ander is niet erg zinvol. We zullen zien dat er tal van ongerijmdheden zullen optreden. Dit doet vermoeden dat we een paar verkeerde aannames doen. Immers het model van Stefan-Boltzmann is aan zich correct. Het gaat om stralingsenergie. De zon straalt in, de aarde straalt uit, er zet zich een evenwicht in en dan kun je de gemeten gemiddelde temperatuur van het oppervlakte van de Aarde vergelijken met de door het model berekende waarde. Als beide kloppen heeft de Aarde dan een broeikaseffect nodig? Naast het gangbare model vergelijken we een door mij afgeleid model en energiebalans. We zullen zien dat het gangbare model en de daarbij horende energiebalans er behoorlijk naast zitten op een heleboel punten. Opnieuw zullen we de gemeten temperatuur vergelijken met de berekende temperatuur en ons de vraag stellen dat als beide gelijk aan elkaar zijn er nog wel sprake is van een broeikaseffect. Is het broeikaseffect niet volstrekt overbodig als je dit moeiteloos voor elkaar krijgt en er geen ongerijmdheden meer optreden maar alle puzzelstukjes nu op hun plaats vallen? We zullen kijken hoe ver we hier mee komen. We zullen het artikel afsluiten met de conclusies die logisch uit het onderzoek volgen.
Het gangbare model
In het gangbare model gaat men er van uit dat een schijf zonne-energie met een oppervlakte van π r2 gelijkmatig wordt verdeelt over het oppervlakte van de Aarde met als oppervlakte 4 π r2. Dat betekent dat een vierkante meter van de Aarde gemiddeld een kwart van de zonne-energie ook wel TSI genaamd in principe ter beschikking staat. Van uit deze aanname gaan we het model uitwerken;
In evenwicht geldt;
I E_in=E_uit Ingaande energie is gelijk aan uitgaande energie
II E_in=(1-α)¼ TSI en E_uit=εσT_gem4 met T_gem=de gemeten gemiddelde temperatuur
III substitutie van II in I geeft;
(1-α)¼ TSI = εσT_gem4
IV T_gem =4√((1-α)¼ TSI / εσ) met T_gem berekend uit de formule
Met; TSI = zonneconstante = 1368 W/m2
α = albedo = 107/342=0,3129
ε=emissiviteit en is vastgesteld op (nagenoeg) 1
σ=Stefan-Boltzmann constante = 5,67*10-8
Het gaat er nu om de gemeten T-gem te vergelijken met de berekende T-gem. De gemeten waarde is gelijk aan 15 °C, de berekende waarde is echter maar -19 °C. Dat is een heel groot verschil. Het verhaal gaat dat dit verschil voor rekening komt van het broeikaseffect dat dus bestaat en waarvan de grootte bepaald kan worden namelijk op 34 °C. Het broeikaseffect berust op de aanname dat zonne-energie vanaf de top van de atmosfeer nagenoeg ongehinderd het oppervlakte weet te bereiken maar dat de warmtestraling die de Aarde vanaf het oppervlakte naar de top van de atmosfeer probeert te stralen nagenoeg niet in staat is om dit te doen. De energie blijft dan hangen en maakt het oppervlakte van de aarde warmer dan het zonder het broeikaseffect zou zijn geweest. Het lijkt allemaal heel mooi te kloppen maar uit de energiebalans die bij dit gangbare model hoort, komen een aantal ongerijmdheden voor. De benodigde emissiviteit wordt bepaald door de uitstraling van het oppervlakte van de Aarde naar de top van de atmosfeer. Zie figuur 1;

Figuur 1 – De energiebaslans van Kiehl en Trenberth(K&T)
Uit de energiebalans van K&T kunnen we afleiden dat van de 390 W/m2 die het oppervlakte van de Aarde uitstraalt uiteindelijk via allerlei omwegen 235 W/m2 weet te ontsnappen naar het heelal. Dit geeft een relevante emissiviteit die veel lager uitvalt dan 1. Immers ε = 235/390=0,6026. Dit is aanzienlijk meer dan nagenoeg niets. Ook blijkt dat zonne-energie niet ongehinderd het oppervlakte weet te bereiken. Van de 342 W/m2 bereikt maar 168 W/m2 het oppervlakte en dat is slechts 49%. Zo verschrikkelijk goed werkt de broeikas blijkbaar ook weer niet. Dit is alvast een beetje vreemd. Wat is nu de emissiviteit? Heeft het de waarde van nagenoeg 1 zoals in het gangbare model is gebruikt of is het 0,6026 zoals uit de energiebalans kan worden afgeleid. Het kan niet allebei zijn. Als we de waarde van 0,6026 invullen in het model dan klopt de berekende temperatuur wel en is dan 15 °C. Bestaat het broeikaseffect opeens niet meer omdat de gemeten waarde van de temperatuur wel overeen komt met de berekende waarde? Het is duidelijk dat we er zo niet uit zullen komen. Zo eenvoudig als het leek is het blijkbaar toch niet. Vandaar de noodzaak om een alternatief model af te leiden. Een model dat hopelijk deze ongerijmdheden weet op te lossen.
Ontwikkelen van een alternatief model
Het door mij afgeleide model gaat er van uit dat de ongerijmdheid van het gangbare model zit in de aanname dat je de schijf zonne-energie gelijkmatig over het oppervlak van de Aarde kunt verdelen. Dit kan dus niet. Het is fysiek onmogelijk. De schijf zonne-energie kan bijvoorbeeld alleen over de dagkant van het oppervlakte van de Aarde worden verdeeld. Dit levert het bekende dag-nacht-ritme op. Ook heb je te maken met de wel bekende seizoenspatronen. Maar de voornaamste reden waarom deze aanname absurd is zit hem in het feit dat de vorm van de Aarde een bol is. In de tropen staat de zon veel hoger aan de hemel dan in de poolgebieden. De tropen krijgen dus veel meer zonne-energie dan de poolgebieden. Daardoor zijn de tropen ook veel warmer. Alleen een omvangrijk energietransport van de tropen naar de poolgebieden kan verhinderen dat de temperatuur daar in de winter volledig ineenstort. Hier zien we dus dat zonne-energie zeer ongelijkmatig wordt verdeeld over het oppervlakte van de Aarde. Willen we weten hoeveel zonne-energie de Aarde werkelijk gemiddelde per vierkante meter ontvangt resteert ons niets anders dan dit per breedtegraadband te achterhalen. Daarbij zullen we zien dat we gebruik dienen te maken van het gewogen gemiddelde. Het oppervlakte van de tropen is veel groter dan dat van de poolgebieden. Zonder weging zouden de lage temperaturen van de poolgebieden te zwaar mee wegen en de hogere temperaturen juist te laag. Dan krijg je een te lage waarde voor het gemiddelde van de temperaturen van de Aarde. Tabel I geeft weer hoe dit uitpakt;

Tabel I – Vaststellen van de gewogen gemiddelde hoeveelheid zonne-energie
Dit is een deel van een grotere tabel die de weergave is hoe mijn globaal model met een dagkant en een nachtkant er uitkomt te zien als je het uitgesplitst naar de breedtegraad. Het is hier dat ik een andere ongerijmdheid op het spoor kom. Volgens het globale model is de hoeveelheid zonne-energie 684 W/m2 maar voor het naar breedtegraad uitgewogen gemiddelde is de waarde 1073 W/m2. Als je deze situatie krijgt van twee verschillende waarden voor een variabele zijn er maar twee mogelijkheden van toepassing. Of een van de twee is juist of ze zijn allebei fout. Maar ze kunnen nooit allebei juist zijn. Om te bepalen welke waarde vermoedelijk juist is eerst een korte uitleg over de tabel. dat is wel op zijn plaats. De eerste kolom is een weging voor het feit dat we hier met breedtegraadbanden werken. De band voor evenaar loopt van +5 tot -5 graden. Dan houdt je op het eind een band over van 85 tot 90 graden. Deze laatste band hoort dan minder mee te wegen omdat het kleiner is. De tweede kolom corrigeert voor het feit dat het oppervlakte van de tropen veel groter is dan dat van de poolgebieden. Als je niet corrigeert voor de beide genoemde effecten klopt de uitkomst niet. De temperaturen vallen ongewogen veel lager uit dan dat ze horen te zijn. Dankzij de wegingen klopt het weer met wat het hoort te zijn. Kolom drie geeft de breedtegraadbanden aan. Kolommen vier en vijf geven per breedtegraadband maar ook globaal de gemiddelde waarden aan voor de maximum temperaturen en de minimum temperaturen. Het eerste is de gemiddelde temperatuur van de dagkant en de tweede is de gemiddelde temperatuur van de nachtkant. Kolom zes geeft het verschil weer tussen de dagkant en de nachtkant. Het verschil is voor de Aarde heel beperkt. De voor dit verhaal belangrijkste kolom is zeven. Via de Lambertus cosinus regel geef je aan hoeveel zonne-energie per vierkante meter per breedtegraadband beschikbaar is aan zonne-energie. Ook hier dien je het gewogen gemiddelde toe te passen om tot een juiste uitkomst te komen. De uitkomst mag gerust verrassend genoemd worden.
Het gewogen gemiddelde voor de hoeveelheid zonne-energie valt veel hoger uit dan in het gangbare model is aan genomen. Het maakt een groot verschil of je de hoeveelheid zonne-energie gelijkmatig verdeelt of dat je de juiste verdeling uitgesplitst naar de breedtegraadband neemt. Het verschil voor de dagkant bij het globale model dat de zonne-energie gelijkmatig verdeeld over de dagkant (684W/m2) en het gewogen gemiddelde (1073 W/m2) bedraagt maar liefst 57%. Dat is aanzienlijk meer dan gedacht. En dit heeft natuurlijk gevolgen. Het gangbare model zal aangepast dienen te worden zodat het overeenkomt met de juiste hoeveelheid zonne-energie. Ook de energiebalans zal opnieuw op gemaakt moeten worden. Eveneens met de juiste hoeveelheid zonne-energie. Daar gaan de volgende paragrafen over.
Aangepast model
Tijd om het gangbare model aan te passen. De eerste aanpassing is voor de hoeveelheid zonne-energie die dus maar liefst 57% hoger blijkt te zijn dan gedacht. Laten we dit als eerste aanpassen. In het gangbare model was de hoeveelheid zonne-energie 342 W/m2. Voeg daar de correctie aan toe voor 57% extra en je krijgt een hoeveelheid van 536 W/m2. Dit is onze aangepaste hoeveelheid voor de zonne-energie. Vandaar zien we wel verder.
Ook voor het aangepast model geldt dat in evenwicht;
I E_in=E_uit
II E_in=(1-α)ZE met ZE de gewogen gemiddelde zonne-energie = 536 W/m2
α de albedo = 0,3129
E_uit=εσT_gem4 met T_gem=de gemeten gemiddelde temperatuur=15°C
ε de emissiviteit = (nagenoeg) 1
σ de Stefan-Boltzmann constante = 5,67*10-8
III substitutie van II in I geeft;
(1-α)ZE = εσT_gem4
IV T_gem =4√((1-α)ZE / εσ) met T_gem berekend uit de formule
Om de T_gem te kunnen berekenen dienen we eerst te weten wat de waarde van de emissiviteit is. Deze hebben we in het gangbare model afgeleid uit de energiebalans van Kiehl & Trenberth. Deze energiebalans zullen we ook dienen aan te passen aan de veel hoger dan verwachte hoeveelheid zonne-energie. Dit doen we in de volgende paragraaf.
Aangepaste energiebalans
We gaan uit van de bestaande energiebalans van Kiehl & Trenberth en voegen hier de noodzakelijk geworden wijzigingen door. De gemiddelde hoeveelheid zonne-energie per vierkante meter is, zo als vastgesteld niet 342 W/m2 maar 536 W/m2. We gaan er van uit dat de verhoudingen voor reflectie door de atmosfeer en oppervlakte en de absorptie door de atmosfeer voor de invallende zonne-energie correct zijn. Hieruit leiden we dan de waarden af voor de aangepaste energiebalans.
α_atm=77/342=0,2251. De werkelijke hoeveelheid invallende zonne-energie is 536 W/m2. Dus de hoeveelheid reflectie door de atmosfeer wordt dan 0,2251*536=121 W/m2. De absorptie van de atmosfeer=67/(342-77)=67/265=0,2528. De aangepaste hoeveelheid voor de absorptie van de atmosfeer is dan 0,2528*(536-121)=105 W/m2. De reflectie waarde door het oppervlakte van α_opp=30/(342-77-67)=30/198=0,1515. Voor de aangepaste energiebalans wordt door het oppervlakte gereflecteerd 0,1515*(536-121-105)=47 W/m2. Dan blijft er voor de absorptie van het oppervlakte een hoeveelheid zonne-energie over van 263 W/m2. Dat is iets minder dan de helft van de hoeveelheid zonne-energie waar we mee begonnen van 536 W/m2. Immers 536-121-105-47 levert een hoeveelheid op van 263 W/m2. We nemen aan dat de hoeveelheden energie voor thermals and evapo-transpiration gelijk blijft. Deze is immers een functie van de temperatuur zoals gemeten en die blijft verder het zelfde in de aangepaste energiebalans. Wat we dan overhouden voor uitstraling van het oppervlakte is dan 263-24-78=161 W/m2. Maar een oppervlakte met een temperatuur van 15°C en een emissiviteit van (nagenoeg) 1 straalt veel meer uit dan 161 W/m2 namelijk 390 W/m2. Het verschil van 390-161=229 W/m2 is dus de hoeveelheid energie die de atmosfeer terug straalt naar de Aarde. Ook de atmosfeer of beter gezegd de troposfeer is een voorwerp in de zin van het model van Stefan-Boltzmann. Het straalt energie uit op grond van de emissiviteit gelijk gesteld op 1 en de gemiddelde temperatuur van de troposfeer. De hoeveelheid energie die de troposfeer terug straalt komt overeen met een gemiddelde temperatuur van de troposfeer van ca -20°C. Dit klopt dus nu ook. In de energiebalans van het gangbare model ging men uit van een terugstraling van 324 W/m2. Dat is veel te hoog. Ook deze ongerijmdheid is opgelost. Wat we nu nog willen weten is wat de hoeveelheid langgolvige straling is die de Aarde terug straalt het heelal in. Dit is in evenwicht de hoeveelheid zonne-energie minus de hoeveelheid gereflecteerde energie. Dus 536-121-47=368 W/m2. Dit alles zetten we in een simpel figuur voor de overzichtelijkheid. Zie figuur 2;

Figuur 2 Aangepaste energiebalans
Het eerste wat we dienen te doen is het figuur te toetsen op de evenwichtsvoorwaarde. Daarvoor kijken we of de ingaande energie gelijk is aan de uitgaande energie. We beginnen met de top van de atmosfeer: De ingaande energie is 536 W/m2. De uitgaande energie is 121+47+368=536 W/m2. Dit klopt. Daarna controleren we voor het oppervlakte: 263+229= 24+78+390 oftewel 492=492 W/m2. Ook dit klopt. Dan blijft over de atmosfeer: 105+24+78+390=229+368 oftewel 597=597 W/m2. Ook dit klopt. Er is dus voldaan aan de evenwichtsvoorwaarde dat ingaande energie gelijk is aan uitgaande energie. En dat is de basis van het Model van Stefan-Boltzmann. Hieruit kunnen we dan uiteindelijk de emissiviteit afleiden van het oppervlakte naar de top van de atmosfeer. Dit levert op dat ε = 368/390=0,9436. En dit komt veel beter overeen met de aanname in het gangbare model dat de emissiviteit nagenoeg 1 is. Dat was in de energiebalans van het gangbare model beslist niet het geval. Ook hier is een ongerijmdheid opgelost. Wat levert dit op voor de berekening van de gemiddelde temperatuur? De gemiddelde temperatuur van het oppervlakte van de Aarde is nagenoeg gelijk aan de gemeten waarde van 15°C. Ook hier is de ongerijmdheid van het gangbare model opgelost. Natuurlijk mag men er van uit gaan dat het Stefan-Boltzmann model in staat is om uit een evenwicht situatie tussen invallende en uitgaande energie de correcte temperatuur te bepalen. De beide heren behoorden tot de knapste koppen van hun tijd. Ze hadden wel iets beters te doen dan modelletjes in elkaar te prutsen die tot niet meer in staat waren dan het bepalen van effectieve temperaturen die geen enkele overeenkomsten hebben met de gemeten temperaturen. Toch zijn nog niet alle vragen beantwoord. Er blijft vooral 1 vraag over. Heeft de aarde nu wel of niet een broeikaseffect en hoe bepaal je zoiets? Hier heb je een algemene formule voor nodig. Daar over gaat de volgende paragraaf.
Algemene formule
Om vast te stellen of de Aarde nu wel of niet een broeikaseffect heeft heb je een algemene formule nodig. Deze kun je afleiden uit het Stefan-Boltzmann model.
In evenwicht geldt;
I E_in = E_uit
II E_in = (1-α)*ZE en E_uit = εσT_gem4
Substitutie van II in I geeft;
III (1-α)*ZE = εσT_gem4
IV (1-α) – ε* [σT_gem4/ZE] = 0
Het gaat om de term tussen de rechte haken. Deze term geeft als het ware aan of de gemiddelde temperatuur van het oppervlakte van de Aarde wel of niet verklaart kan worden vanuit de gemiddelde hoeveelheid zonne-energie per vierkante meter die beschikbaar is. Dit gaan we nu uitproberen voor zowel het gangbare model als wel voor het aangepaste model. Het resultaat staat in tabel III;

Tabel II – Vergelijking tussen het gangbare model en het aangepaste model
Als de term tussen rechte haken groter dan 1 is wil dit zeggen dat de gemiddelde temperatuur van het oppervlakte van de Aarde eigenlijk te warm is dan op grond van de hoeveelheid beschikbare zonne-energie aannemelijk is. In het gangbare model is de term groter dan 1. Daar is dus een broeikaseffect aanwezig. Maar in het door mij aangepast model beslist niet. De gemiddelde temperatuur van het oppervlakte van de Aarde is prima te verklaren met de hoeveelheid beschikbare zonne-energie. Hiermee is het pleit beslist. En de algemene formule en de vastgestelde ongerijmdheden in het gangbaar model maken duidelijk dat de Aarde geen broeikaseffect heeft. Dat heeft de Aarde ook helemaal niet nodig. Dus waarom daar nog langer aan vast willen houden.
Vragen en antwoorden
Heeft de Aarde een broeikaseffect en hoe groot is dit dan?
Volgens de gangbare model heeft de Aarde het wel en is het 34°C groot. In het aangepaste model en energiebalans zien we dat de backradiation van de atmosfeer nagenoeg gelijk is aan wat een voorwerp in de zin van het Stefan-Boltzmann model met een emissiviteit van 1 en een gemiddelde temperatuur van -21°C aan straling uitzendt. Dus nee, in het aangepaste model is nagenoeg geen ruimte voor een broeikaseffect. Ook de emissiviteit van het oppervlakte naar het heelal is indirect nagenoeg gelijk aan 1. Ook hier is weinig tot geen ruimte voor een broeikaseffect. De gemeten temperatuur komt nagenoeg overeen met de door het aangepaste model berekende temperatuur. Ook hier dus vrijwel geen ruimte voor een broeikaseffect. Ook de algemene formule wijst in deze richting. De gemiddelde temperatuur van het oppervlakte van de Aarde kan prima verklaard worden uit de hoeveelheid beschikbare zonne-energie. Er is geen noodzaak voor het aannemen dat de Aarde een broeikaseffect heeft.
Waarom heeft de Aarde geen broeikaseffect?
Daar zijn twee goede redenen voor. Ten eerste blijkt dat de gemiddelde hoeveelheid zonne-energie veel hoger (maar liefst 57% meer) is dan in het gangbare model verondersteld wordt. En dit allemaal omdat men een volkomen absurde aanname doet dat een schijf zonne-energie gelijkmatig verdeeld kan worden over het oppervlakte van de Aarde. Dat kan dus niet. Het is fysiek onmogelijk en ook van de Aarde kan het onmogelijke niet verlangd worden. Het naar de breedtegraad gewogen gemiddelde geeft de juiste waarde aan. Een andere reden vindt men terug in tabel II;
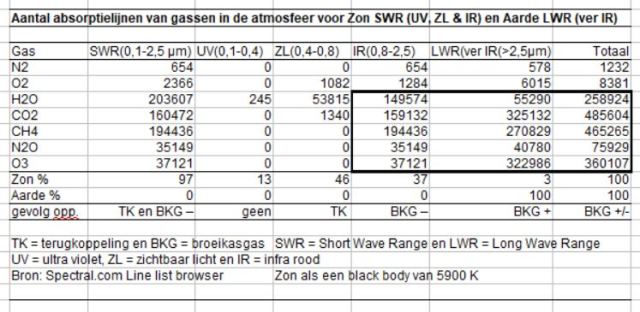
Tabel III – Absorptielijnen in het SWR en LWR gebied
Broeikasgassen zoals kooldioxide (CO2) absorberen inderdaad op grote schaal de warmtestraling die de Aarde van het oppervlakte naar de top van de atmosfeer uitzendt maar absorbeert eveneens op grote schaal het infrarode deel van de zonne-energie die van de top van de atmosfeer probeert naar het oppervlakte te komen. De beide vormen van absorptie heffen elkaar op voor het oppervlakte van de Aarde. In het verre infrarood wordt massaal straling tegengehouden die de top van de atmosfeer probeert te bereiken maar in het infrarode deel wordt net zo massaal verhinderd dat straling het oppervlakte bereikt. Dat is de reden waarom het broeikaseffect niet zo heel erg goed werkt. Beide effecten heffen elkaar blijkbaar op. Zodat er netto weinig over blijft voor het bestaan van een broeikaseffect.
Waarom wordt de Aarde dan warmer door stijging van het gehalte van broeikasgassen in de atmosfeer?
Beide genoemde effecten heffen elkaar zoals gezegd wel op voor het oppervlakte maar niet voor de atmosfeer. Beide vormen van absorptie zorgen er voor dat de atmosfeer op warmt. Daardoor zal het meer straling terug sturen van de atmosfeer naar het oppervlakte. De backradiation neemt toe en dit geeft extra energie voor het oppervlakte dat hierdoor opwarmt. Doordat het oppervlakte opwarmt zal het op zijn beurt meer energie gaan uitstralen die door de atmosfeer weer geabsorbeerd wordt. Deze zal dan weer opwarmen en meer straling terug zenden. Dit is een vorm van positieve terugkoppeling. Het versterkt het primaire proces dat een toename van broeikasgassen leidt tot meer absorptie door de atmosfeer die daardoor opwarmt en meer straling terug stuurt naar het oppervlakte van de Aarde. Maar dit proces dient men niet te verwarren met het versterkt broeikaseffect. Zoals we in dit artikel immers hebben aan getoond, de Aarde heeft geen broeikaseffect en niet bestaande effecten kun je niet versterken. Maar er bestaat een sterke samenhang tussen bijvoorbeeld het kooldioxide gehalte van de atmosfeer en de temperatuurstijging van de Aarde. Dit hoop ik in een volgend artikel aan te tonen.
Zijn er antwoorden gegeven op de gestelde vragen?
Ja. Er zijn uiteindelijk wel degelijk antwoorden gevonden op de vragen die in de inleiding zijn gesteld. De stukjes van de puzzel beginnen op hun plaats te vallen. De ongerijmdheden die we tegen kwamen in ons onderzoek zijn opgelost. Ze waren ontstaan door vreemde aannamen die helemaal niet nodig waren. Je hebt geen broeikaseffect nodig om de opwarming van de Aarde door een stijging van broeikasgas te verklaren. Het gaat prima zonder. Weg met dit artefact. Het is mijn overtuiging dat de klimaatwetenschappers in het verleden de term puur metaforisch hebben bedoeld.
Conclusies
Het broeikaseffect blijkt voor de Aarde niet te bestaan. Het kwam voort uit een aantal verkeerde aannames over bijvoorbeeld de hoeveelheid zonne-energie per vierkante meter die beschikbaar zou zijn. De beschikbare hoeveelheid blijkt veel groter te zijn. Het is gelukt om allerlei ongerijmdheden uit het model en de energiebalans te halen. Met de juiste waarden voor de relevante variabelen kan men prima de gemiddelde temperatuur van de Aarde bepalen zonder gebruik te hoeven maken van een broeikaseffect. Ook blijkt het wel degelijk mogelijk is om de Aarde te laten opwarmen bij een toename van bijvoorbeeld kooldioxide. Ook hier is het (versterkt) broeikaseffect niet nodig. Het lijkt er op dat de klimaatwetenschap het slachtoffer werd van het letterlijk nemen van wat de klassieke wetenschappers alleen metaforisch bedoeld hebben. Er lijkt inderdaad een algemene formule uit het Stefan-Boltzmann model te kunnen worden afgeleid die ons verteld dat er wel of niet een broeikaseffect bestaat. Ongeveer alles wat ik geschreven heb de afgelopen jaren zal herschreven dienen te worden. Dat is jammer maar niet erg. Science is never settled. Gelukkig maar want wat zouden we dan moeten doen? Kan het broeikaseffect elders bijvoorbeeld op Venus wel bestaan? Dat weet ik niet. Dit heb ik niet onderzocht. Hier lijkt meer onderzoek nodig. Daar zou je een leuk artikel over kunnen schrijven. Misschien dat ik er ooit de tijd voor vindt buiten mijn andere drukke bezigheden. Ik ben maar een amateur parttime onderzoeker. Maar als liefhebber van het uitzoeken van zaken zal ik zeker proberen om nog meer dingen uit te zoeken. Wat zou ik anders met mijn schaarse tijd moeten aanvangen.
Literatuurlijst
Bestaat het broeikaseffect eigenlijk wel?
Het broeikaseffect bestaat wel (Het afleiden van de formule)
Een Stefan-Boltzmann model voor planeten en hun satellieten
Uitbreiding van het model naar de breedtegraden
Is een Maan met Aardse eigenschappen een zinvol concept
Earth’s Annual Global Mean Energy Budget(pdf) – J.T. Kiehl and Kevin E. Trenberth
Wikipedia – Gewogen gemiddelde
Wikipedia – Lambert’s Cosinus regel
Klimaatverandering – Toename van CO2 versterkt het broeikaseffect

Heel interessant maar moeilijke materie
LikeGeliked door 1 persoon
Het artikel is een stap in de goede richting maar heeft als manco dat alleen gekeken wordt naar de hoeveelheid zonne-energie voor 12 uur s-middags. Je dient te kijken naar het gemiddelde voor de hele dag. Daar voor is het nodig om een matrix te maken die fijn genoeg is om dit aan te kunnen. Daar ben ik op het moment mee bezig. het is veel werk maar daar heb ik de tijd voor. Zo gauw dit af is zal ik een nieuw artikel plaatsen en aantonen dat ik gelijk heb. De aarde heeft geen broeikaseffect nodig. De Aarde is helemaal niet te warm in verhouding tot de gemiddelde hoeveelheid zonne-energie. De hoeveelheid is verkeerd zoals dit artikel weer geeft. Maar zoals we op school al wisten; Hebben is hebben en krijgen s de kunst.
LikeLike
Pingback: Heeft de Aarde nu wel of niet een broeikaseffect – Deel 1 – De rekensommen | Raymond FANTASTische Horstman
Pingback: Vergelijkingen | Raymond FANTASTische Horstman
Pingback: Naakt lopen, kolonialisme, klimaatcrisis, cultuur en vooroordeel – Jeshuaisten / Jeshuaists
Pingback: Gaan we van een vagevuur naar een hel – Some View on the World